Achievement
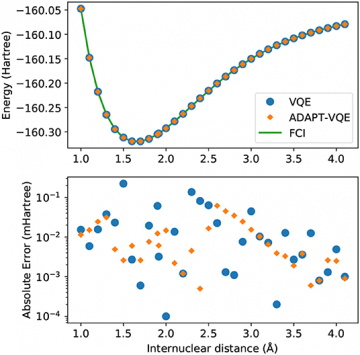
A team of ORNL scientists have investigated the accuracy of quantum computing methods to calculate the electronic ground states and potential energy curves for selected diatomic molecules, namely H2, NaH, and KH. Using numerical simulation, they found multiple methods provide good estimates of the energy and ground state, but only some methods were shown to be robust to the underlying optimization methods. An important finding from this work is that current, gradient-based optimizations is more economical and delivers superior performance than analogous simulations carried out with gradient-free optimizers. The results also identify small errors in the prepared state fidelity which show an increasing trend with molecular size.
Significance and Impact
The long-term success of quantum computing will depend on the efficiency with which the algorithms solve important problems, and this work addresses the question of what makes a good algorithm for electronic structure calculations from quantum chemistry. While the results are limited to the ground-states of diatomic molecules solved using noiseless simulation, they provide ground truth for how well such variational methods may perform. In addition, this work supports the broader goal of establishing a diverse library of quantum algorithms.
Research Details
We benchmark the adaptive variational quantum eigensolver prescriptions, ADAPT-VQE in particular, by comparing the prepared quantum states with the conventional solutions obtained from exact diagonalization of the full configuration interaction Hamiltonian. We track the energy of the minimized expectation value as well as the fidelity of the corresponding prepared state using multiple ansatzes, optimization methods, and molecular Hamiltonians. We calculate infidelity as a measure of error for the prepared quantum state relative to the expected, exact result from quantum chemistry using frozen-core Hamiltonians. Across these examples, we find that ADAPT-VQE is the more robust method due mainly to its performance with respect to optimization methods. While all methods lead to small errors as measured by the infidelity, these errors are found to grow with molecular size.
Overview
The variational quantum eigensolver strives to recover the lowest-energy eigenvalue of a given Hamiltonian by preparing quantum states guided by the variational principle. In practice, the prepared quantum state is indirectly assessed by the value of the associated energy. Novel adaptive approaches have now established a clear connection between the theory of quantum chemistry and the quantum state ansatz used to solve the electronic structure problem. Using numerical simulation, ORNL has found multiple methods provide good estimates of the energy and ground state, but only some methods were shown to be robust to the underlying optimization methods. An important finding from this work is that current, gradient-based optimizations is more economical and delivers superior performance than analogous simulations carried out with gradient-free optimizers. The results also identify small errors in the prepared state fidelity which show an increasing trend with molecular size.
Last Updated: February 24, 2021 - 1:18 pm