Achievement
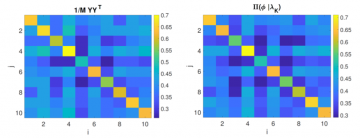
We devised a method to estimate and quantify the uncertainty of states output by quantum physical simulators. In our method, sequential Monte Carlo (SMC) is used to sample from the maximum entropy distribution consistent with the low-order moments of the observed outputs. This readily yields quantities such as a maximum likelihood estimates and marginal distributions. We demonstrate the effectiveness of this method by simulating the reconstruction and uncertainty quantification of a random Ising model involving 10 spin qubits.
Significance and Impact
Near-term quantum computers hold promise for simulating materials, molecules, and other quantum physical systems, but their outputs must be carefully interpreted due to noise and other device imperfections. A challenge is that the output distributions of such physical simulations cannot feasibly be measured or calculated in full. We address this challenge using modern Bayesian sampling techniques to estimate parameters of a plausible posterior distribution consistent with the observations. Our method scales more favorable than prevailing characterization methods and is more principled, constituting an important early step toward extracting meaningful results from near-term quantum physical simulators.
Research Details
- A maximum entropy ansatz is employed for the likelihood within a Bayesian framework for noisily observed moments of the simulator outputs. A debiased estimator of the gradient of the posterior is constructed, and this is used within stochastic gradient Langevin dynamics to sample the posterior.
- If given exact output moments, the maximum entropy distribution is recovered using Robbins Monro stochastic iteration, where unbiased estimators of the (otherwise intractable) fixed point equation are obtained via SMC sampling.
- Both methods are investigated analytically and validated via simulation.
Overview
The problem of estimating certain distributions over {0, 1}d is considered here. The distribution represents a quantum system of d qubits, where there are non-trivial dependencies between the qubits. A maximum entropy approach is adopted to reconstruct the distribution from exact moments or observed empirical moments. The Robbins Monro algorithm is used to solve the intractable maximum entropy problem, by constructing an unbiased estimator of the un-normalized target with a sequential Monte Carlo sampler at each iteration. In the case of empirical moments, this coincides with a maximum likelihood estimator. A Bayesian formulation is also considered in order to quantify uncertainty a posteriori. Several approaches are proposed in order to tackle this challenging problem, based on recently developed methodologies. In particular, unbiased estimators of the gradient of the log posterior are constructed and used within a provably convergent Langevin-based Markov chain Monte Carlo method. The methods are illustrated on classically simulated output from quantum simulators.
Last Updated: May 28, 2020 - 4:06 pm