Achievement
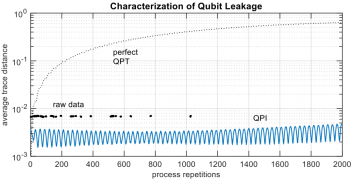
Ryan Bennink and Pavel Lougovski, senior quantum computing researchers at Oak Ridge National Laboratory (ORNL), have developed a more accurate way to characterize the behavior of qubits in quantum computing devices. In this method, a quantum process of interest (such as a basic computational operation) is characterized by probing the qubit state at selected times for a variety of input states. Bennink and Lougovski showed how to process such time-series data to infer a dynamical model involving the qubit and its effective environment. Simulations show that this method is capable of accurately characterizing qubit behavior over long time scales due to realistic device imperfections such as qubit leakage, control drift, and persistent interactions with material impurities.
Significance and Impact
Prior qubit characterization methods have ignored the effect of environment memory. This leads to inaccurate predictions of qubit errors over long time scales. Our team advanced the state-of-the art by developing a characterization method free of this unrealistic assumption. Our characterization method is capable of yielding more accurate models of qubit error processes, paving the way for a more accurate performance assessments of near-term quantum computing devices, as well as enabling better error mitigation techniques based on more complete models of error processes.
Research Details
- The work presents a formalism for representing and a method of empirically characterizing arbitrary quantum dynamics, in particular open quantum systems with non-Markovian dynamics.
- Data collection consists of performing quantum process tomography for various durations of the process.
- The data is arranged into a large matrix with block-Hankel structure. The effective dynamical dimension of the process is estimated using a chi-square test on the singular values of the matrix.
- A dynamical map representing the process is obtained by maximizing the model likelihood. A variety of techniques are employed to robustly solve this exceedingly nonlinear and non-convex constrained optimization problem:
- The likelihood is approximated as a weighted sum of squared errors.
- The core optimization kernel consists of Gauss-Newton steps with line search.
- Constraints are enforced via penalty functions with dynamically adapted weights.
- Progressive optimization avoids local optima by starting with coarse-level data and gradually incorporating fine-level data as the fit improves.
- The method was validated via numerical simulation for several realistic types of qubit error processes including leakage between computational and non-computational states, control drift, and coupling to material impurities.
- Our method is based on a classic systems engineering technique for linear filter realization.
Publication/Citation and DOI:
Ryan S. Bennink and Pavel Lougovski, “Quantum process identification: a method for characterizing non-Markovian quantum dynamics.” New J. Phys. 21 083013 (2019). https://dx.doi.org/10.1088/1367-2630/ab3598
Overview
Established methods for characterizing quantum information processes do not capture non-Markovian (history-dependent) behaviors that occur in real systems. These methods model a quantum process as a fixed map on the state space of a predefined system of interest. Such a map averages over the system's environment, which may retain some effect of its past interactions with the system and thus have a history-dependent influence on the system. Although the theory of non-Markovian quantum dynamics is currently an active area of research, a systematic characterization method based on a general representation of non-Markovian dynamics has been lacking. In this article we present a systematic method for experimentally characterizing the dynamics of open quantum systems. Our method, which we call quantum process identification (QPI), is based on a general theoretical framework which relates the (non-Markovian) evolution of a system over an extended period of time to a time-local (Markovian) process involving the system and an effective environment. In practical terms, QPI uses time-resolved tomographic measurements of a quantum system to construct a dynamical model with as many dynamical variables as are necessary to reproduce the evolution of the system. Through numerical simulations, we demonstrate that QPI can be used to characterize qubit operations with non-Markovian errors arising from realistic dynamics including control drift, coherent leakage, and coherent interaction with material impurities.
Last Updated: May 28, 2020 - 4:02 pm